Yifan Yang (杨轶凡)

Deep Learning Architect at NVIDIA
yifany AT csail.mit.edu
Google Scholar
Github
LinkedIn
Curriculum Vitae
Tensor Core MMA Swizzle Layout
Disclaimer: The content of this blog reflects my personal experiences and opinions while learning GPU programming in my own time. All information presented is publicly available and does not represent the views or positions of NVIDIA Corporation or any of its affiliates.
0. Introduction
The tensor cores in Nvidia GPUs accelerate matrix multiplication operations.
And the tensor cores have particular layout requirement on their input matrices in shared memory (SMEM).
You can’t just feed a row-major or column-major matrix to the tensor core.
It requires the input matrices to follow a specific set of Swizzle Layout.
In this blog, I’ll focus on what these swizzle layout are and how the input matrices are represented in these swizzle layout formats in SMEM.
This is a pre-requisite of even writing a functional MMA kernel using tensor cores. Later in the blog, I’ll touch upon the motivation and performance implications of these swizzle layout.
The logical flow of this blog is a bit different from my other blogs as I try to explain to you how to use the swizzle layout first and then why we need them.
Because I believe being able to write a functional kernel is way more important than the philosophical discussions.
1. Why do I Need to Care about All These?
Isn’t Triton/ThunderKitten/Cutlass already taking care of this complex layout scheme for us? Why would you ever want to manually write/understand it?
That is a very good question and the answer depends on who you are. If you are developer of Triton/ThunderKitten/Cutlass, of course you need to understand this because you are doing the heavy lifting such that the DSL users don’t need to care about swizzle layout.
I belong to the second category where these DSLs don’t perform well on the cases I care about. I write kernels for ultra low latency LLM inference which means we run things at very low batch size. This makes the GEMM/Attention problem size to be rather unconventional and many of these DSLs don’t perform well on these problem sizes. Rather than fixing the DSL compiler, it’s much faster to just manually write the kernel tailored for these problem sizes. But this requires understanding the low level details of how to drive the tensor core and the swizzle layout is one of the key things to understand.
2. Background
Different generations of the tensor core source input matrices from different storage idioms:
- Ampere tensor core (ptx is
mma) source both input A and B matrix from RF. - Hopper tensor core (ptx is
wgmma) source input A matrix from RF/SMEM and input B matrix from SMEM. - Blackwell tensor core (ptx is
tcgen05.mma) source input A matrix from SMEM/TMEM (Tensor Memory) and input B matrix from SMEM.
However, even if some input source are from RF/TMEM, the data are still firstly staged into SMEM (most of the time), and then loaded into RF/TMEM.
And the tensor core has layout requirement on the data in SMEM, i.e. swizzle layout.
2.1. Motivating Example: Ampere MMA
To make our life easier, in this blog we focus on how to write a correct MMA kernel for Ampere tensor core (using mma ptx instructions).
The general idea and specification of the swizzle layout should be the same for hopper and Blackwell tensor cores too.
The mma instruction we pick is mma.sync.aligned.m16n8k8.row.col.f32.bf16.bf16.f32 which does D = A * B + C where A is bf16 [M, K] (row major) and B is bf16 [K, N] (column major) and C/D is f32 [M, N] and M = 16, N = 8, K = 8.
The mma instruction expects both the input and output in the RF (rmem).
We call the per thread register storing the input/output matrix fragment.
Below is the matrix A fragment (Figure 71 of PTX 9.0 doc) of this mma instruction.
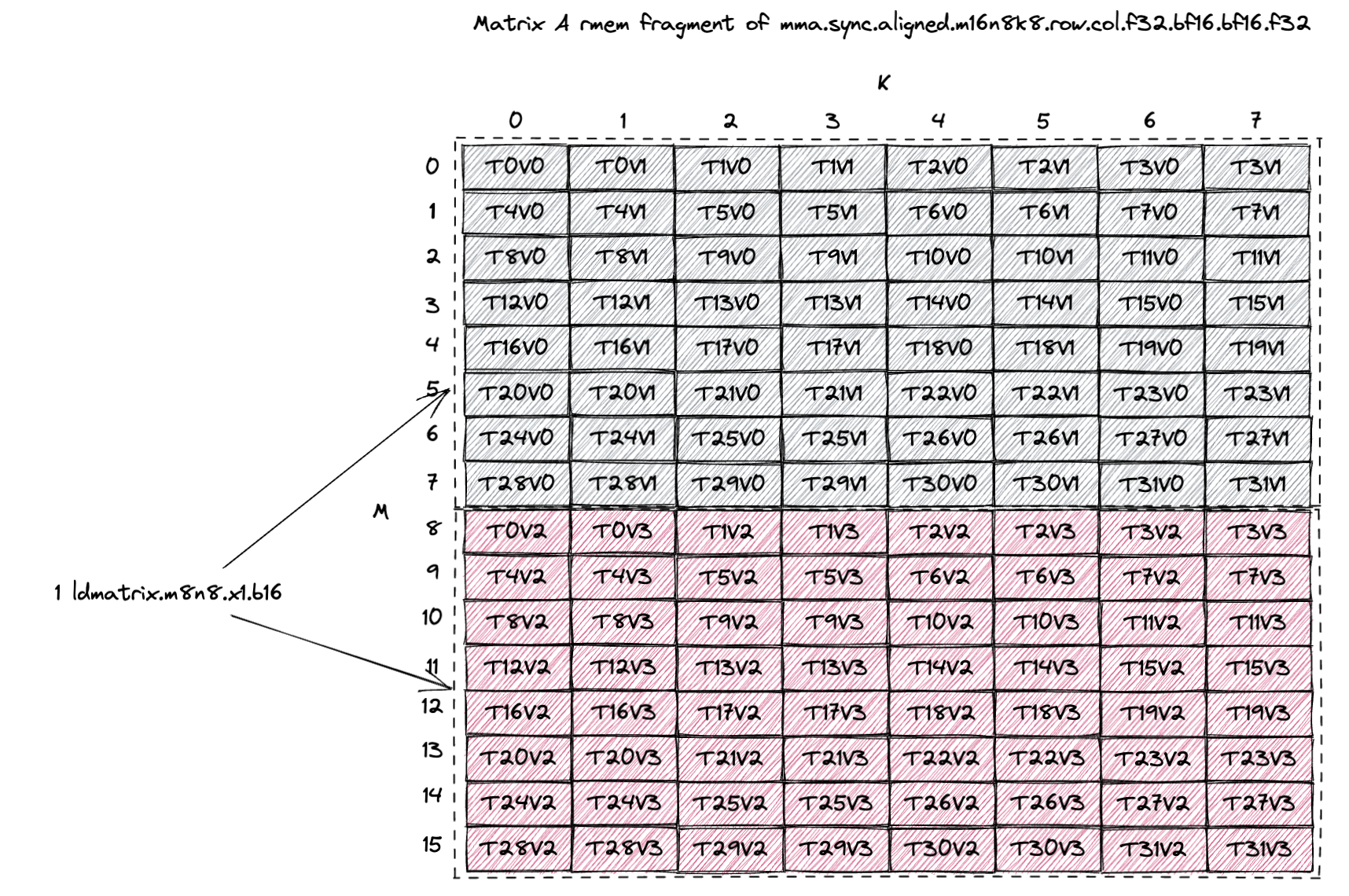
The A tile is [16, 8] and stored in 32 threads, each thread stores 4 elements of the A tile.
The way we load the bf16 A tile from SMEM into RF is via the ldmatrix.m8n8.x1.b16 instruction.
Each call to ldmatrix will load a M=8, K=8 (or a 8x16B) subtile from SMEM into RF.
So the grey color denotes the 8x16B data loaded by the first ldmatrix instruction (2 elements per thread) and the red color denotes the data loaded by the second ldmatrix instruction (2 elements per thread).
Figure 104 of PTX 9.0 doc describes the data layout in the RF after the ldmatrix instruction, which is exactly what we draw above for the grey and red subtile.
This suggests that for whatever layout the A tile is stored in SMEM, it has to support the 8x16B subtile load pattern of ldmatrix.m8n8 at full SMEM read bandwidth (128B/cycle).
The swizzle layout is the exact solution to this requirement.
And we will show below how each and every one of the swizzle layout satisfies this requirement.
2.1.1. Above Example But in CuTe Terminology
Ultimately we will use the mma instruction through CuTe, so it might be good to understand the above layout in CuTe terminology.
The mma atom of mma.sync.aligned.m16n8k8.row.col.f32.bf16.bf16.f32 is SM80_16x8x8_F32BF16BF16F32_TN.
We can draw the fragment layout by using print_svg function and will get the following figure.
A matrix fragment layout is on the bottom left of the figure. B matrix is top right and C matrix is bottom right. We can see the A matrix fragment layout exactly matches the one we manually drew above.
In CuTe, this A matrix fragment layout is called the inverse TV-layout, meaning it represents the coordinate mapping between (M, K) to (T, V).
T stands for thread id and V stands for value id.
T1V2 means the third value in thread 1.
The formula below shows how we derive the stride of the inverse TV-layout.
# inverse TV-layout: (M, K) -> (T, V)
Shape: ((8, 2), (2, 4))
Stride: ((4, 64), (32, 1))
m0 = [0, 8)
m1 = [0, 2)
n0 = [0, 2)
n1 = [0, 4)
A((m0, m1), (n0, n1)) # natural coordinate of tensor
= TV(m0 * 4 + n1, m1 * 2 + n0) # 2d coordinate of TV layout
= TV((m0 * 4 + n1) * 1 + (m1 * 2 + n0) * 32) # 1d coordinate of TV layout
= TV(m0 * 4 + m1 * 64 + n0 * 32 + n1)
The actual TV-layout (mapping from (T, V) to (M, K)) for A matrix fragment can be retrieved by inspecting the ALayout member of the MMA_Traits of the mma atom.
In this particular case, the A TV-layout is SM80_16x8_Row.
The formula below shows how we validate the TV-layout is correct.
# TV layout: (T, V) -> (M, K)
Shape: ((4, 8), (2, 2))
Stride: ((32, 1), (16, 8))
t0 = [0, 4)
t1 = [0, 8)
v0 = [0, 2)
v1 = [0, 2)
TV((t0, t1), (v0, v1)) # natural coordinate of tensor
= A(t0 * 32 + t1 + v0 * 16 + v1 * 8) # 1d coordinate of A layout
= A((t1 + v1 * 8) * 1 + (t0 * 2 + v0) * 16) # 1d coordinate of A layout
= A(t1 + v1 * 8, t0 * 2 + v0) # 2d coordinate of A layout
Note that the above two layouts are inverse of each other, i.e. the inverse of TV-layout is the inverse TV-layout.
We can validate this easily with the following CuTe-DSL code by taking the right_inverse of the TV-layout and will get the inverse TV-layout.
The CuTe C++ code is here.
import cutlass
import cutlass.cute as cute
@cute.jit
def test():
TV = cute.make_layout(((4, 8), (2, 2)), stride=((32, 1), (16, 8))) # (T, V) -> (M, K)
cute.printf("TV: {}\n", TV)
A = cute.right_inverse(TV) # (M, K) -> (T, V)
cute.printf("A: {}\n", A)
if __name__ == "__main__":
test()
3. MMA Swizzle Layout
There are roughly 8 legal SMEM swizzle layout that the ldmatrix/tensor core understands (blackwell introduces 2 new ones but we omit them here for simplicity):
- K-Major Swizzle None (Sec. 3.1.1) (CuTe definition)
- K-Major Swizzle 32B (Sec. 3.1.2) (CuTe definition)
- K-Major Swizzle 64B (Sec. 3.1.3) (CuTe definition)
- K-Major Swizzle 128B (Sec. 3.1.4) (CuTe definition)
- MN-Major Swizzle None (Sec. 3.2.1) (CuTe definition)
- MN-Major Swizzle 32B (Sec. 3.2.2) (CuTe definition)
- MN-Major Swizzle 64B (Sec. 3.2.3) (CuTe definition)
- MN-Major Swizzle 128B (Sec. 3.2.4) (CuTe definition)
Importantly, swizzling doesn’t change the major-ness of the input tile, i.e. if the tile in GMEM is K-major (K dimension is the contiguous dimension), the SMEM tile will still be roughly K-major after swizzling.
No transpose happens during GMEM to SMEM copy.
Transpose happens during SMEM to RF copy (i.e. ldmatrix) (more about this in Sec. 6).
So if the GMEM tile is MN-major, you should choose the MN-major swizzle layout for SMEM.
Section 9.7.16.10.6. Shared Memory Layout and Swizzling of PTX 9.0 doc best describes all these swizzle layout. I basically redraw all the figures with more details and annotations of what’s going on.
3.1. K-Major Swizzle Layout
If the GMEM tile is K-major, you should choose the K-major swizzle layout for SMEM.
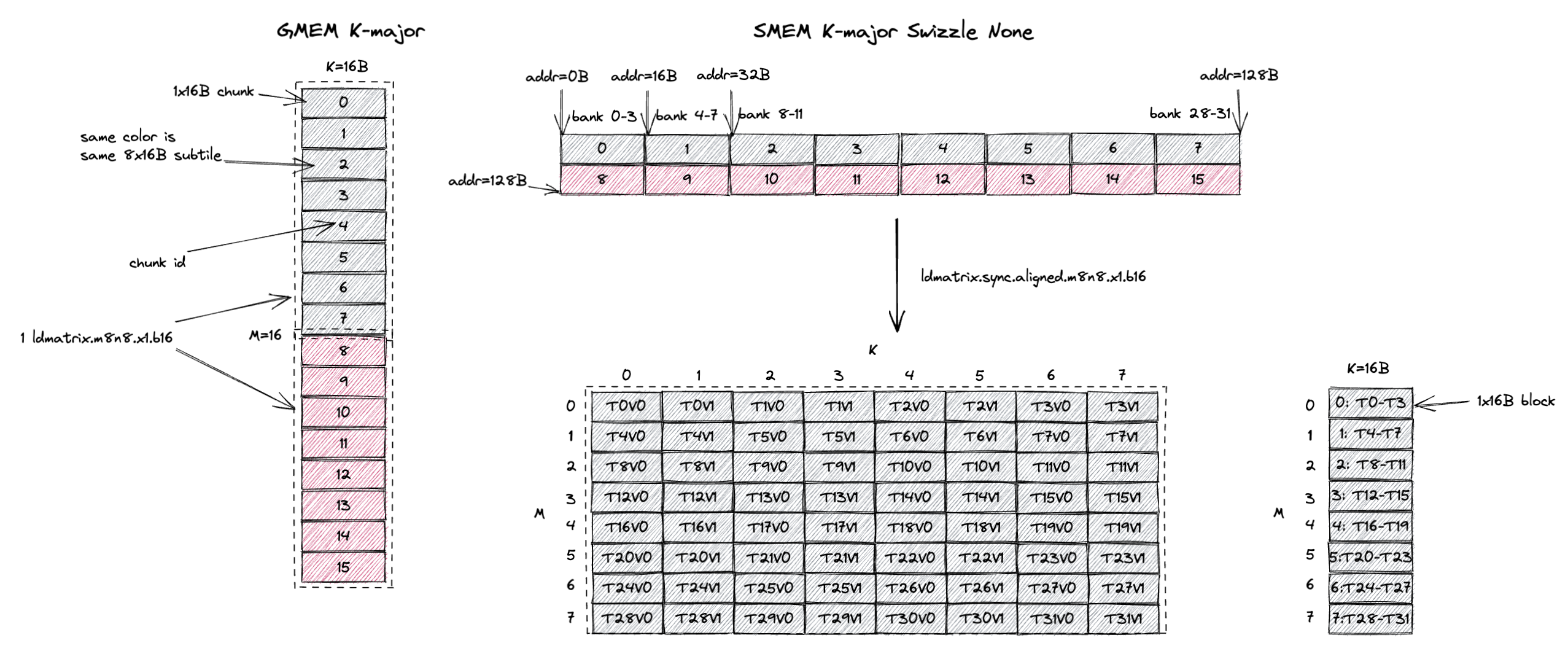
3.1.1. K-Major Swizzle None
The first legal layout is called Swizzle None as illustrated below.
CuTe calls it swizzle interleaved which is probably more accurate, but we follow the naming convention in the PTX 9.0 doc and call it swizzle none.
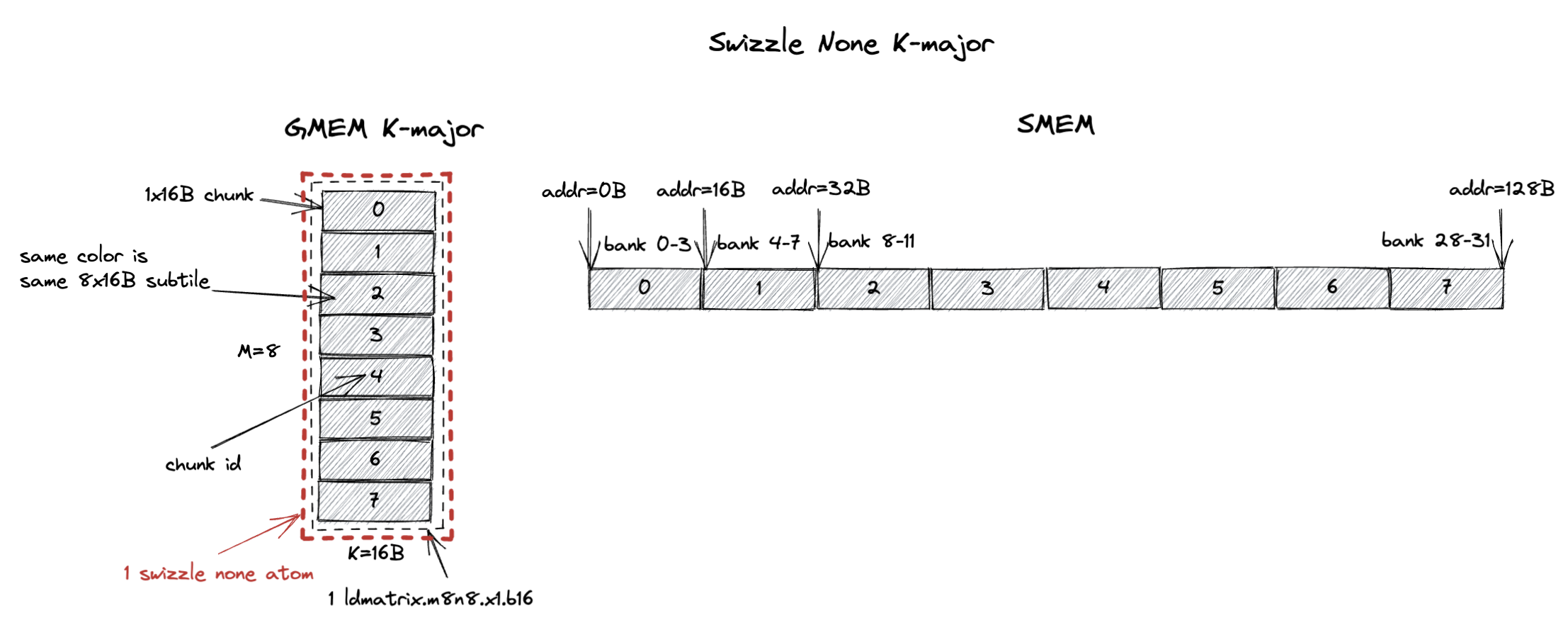
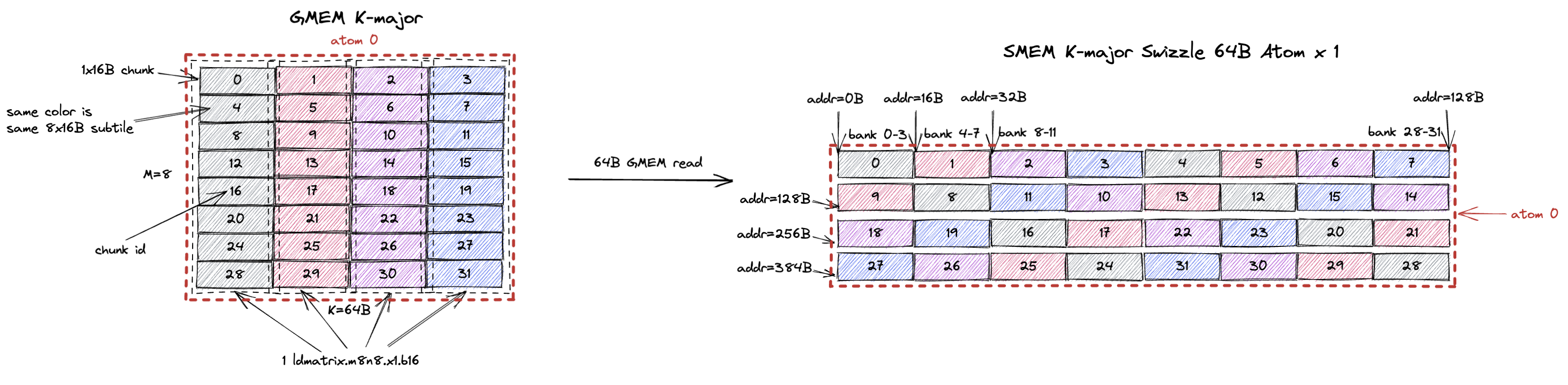
A tile of 8x16B (M=8, K=16B or K=8 assuming bf16 input) in GMEM is shown on the left with each row being a 16B chunk.
In the figure, each grey block is a 1x16B chunk (containing 8 K values) and the 8x16B tile contains 8 chunks from chunk 0 to chunk 7.
These 8 chunks (8x16B) forms what we call the swizzle none atom.
The swizzle none layout specifies that the swizzle none atom is stored contiguously in SMEM with the chunk order shown on the right of the figure.
In this case, chunk 0 is stored at the first 16B in SMEM, chunk 1 is stored at the second 16B in SMEM, and so on.
Note that 8 chunks occupies 128B in SMEM which happens to match the 32 bank (4B/bank) organization of SMEM.
This means chunk 0 resides in bank 0-3, chunk 1 resides in bank 4-7, and so on.
Recall that the swizzle layout should serve the 8x16B load pattern of ldmatrix.m8n8 at full SMEM read bandwidth (128B/cycle).
The swizzle none layout satisfies this requirement.
It happens so that the 8x16B subtile the ldmatrix.m8n8 instruction loads is exactly 1 swizzle none atom.
Since all 8 chunks are stored contiguously in SMEM, the ldmatrix.m8n8 instruction can load all 8 chunks in 1 cycle without bank conflicts.
And the 8x16B subtile is K-major.
Confusingly, swizzle none is not the intuitive linear SMEM layout you would expect because it mandates the M=8, K=8 K major subtile to be stored contiguously in SMEM.
We will explain this more with a concrete example in Sec. 4.
3.1.2. K-Major Swizzle 32B
The swizzle atom becomes bigger with swizzle 32B layout.
It now becomes a 8x32B tile (M=8, K=32B or K=16 assuming bf16 input).
So now you can see the naming convention, K-Major Swizzle 32B implies the swizzle atom is a 8x32B K-major tile.
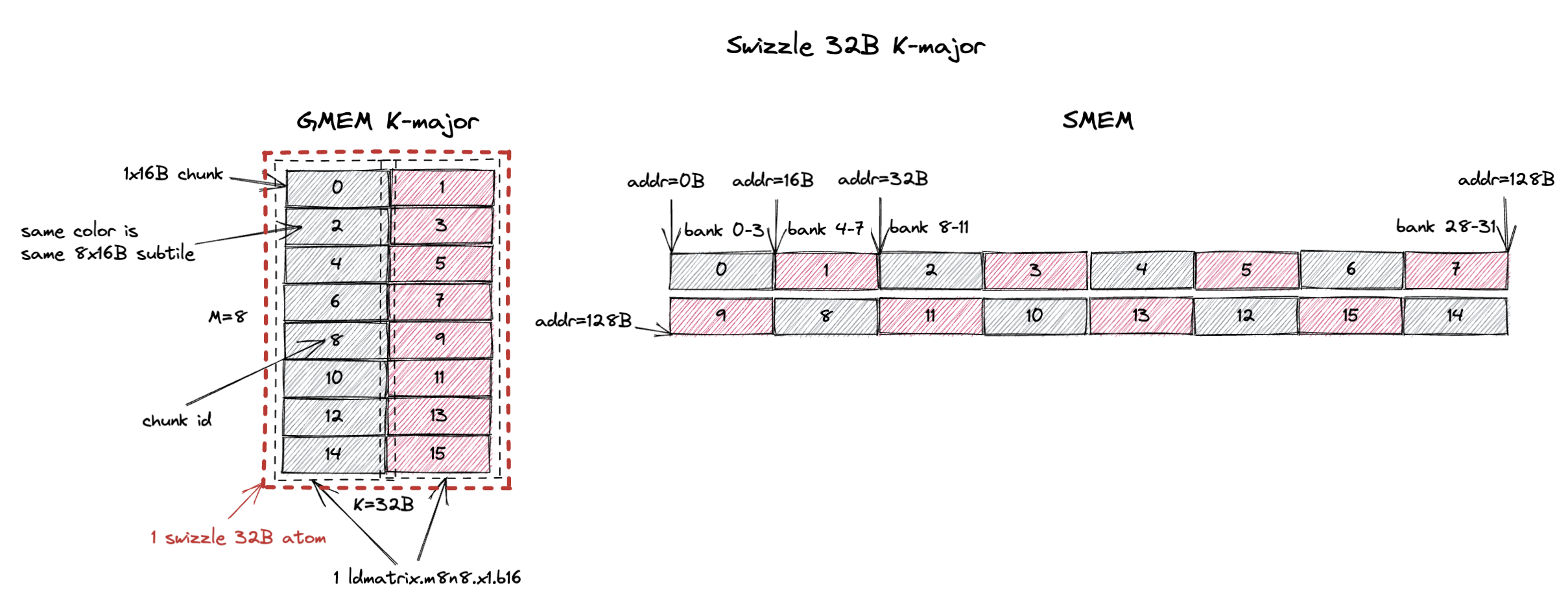
This swizzle 32B atom now contains 16 1x16B chunks or 2 8x16B (required by ldmatrix.m8n8) subtiles.
The swizzle 32B layout specifies that the 16 1x16B chunks in the atom are stored contiguously in SMEM with the chunk order shown on the right of the figure.
Running the same ldmatrix.m8n8 instruction on this swizzle 32B layout, we want to load a subtile of 8x16B at full SMEM read bandwidth (128B/cycle).
The swizzle 32B layout contains 2 such subtiles, colored in grey and red.
The grey subtile contains chunk 0, 2, 4, 6, 8, 10, 12, 14 and the red subtile contains chunk 1, 3, 5, 7, 9, 11, 13, 15.
Because chunks are organized in that particular swizzle order in SMEM, from the figure we can see that loading the grey subtile from SMEM can be done in 1 cycle without bank conflicts.
The same is true for the red subtile.
So the ldmatrix.m8n8 instruction can load both the grey and red subtiles in 1 cycle without bank conflicts.
Finally, we introduce a new concept called 16B atomicity.
This is saying for a 16B chunk that is contiguous in GMEM, it’s also contiguous in SMEM after swizzling.
Our 16B chunk organization is exactly that.
Even though the chunk orders are swizzled in SMEM, the data within each chunk still remains contiguous.
All swizzle layout by default uses 16B atomicity.
There are exceptions with swizzle 128B layout which could allow 32B/64B atomicity (i.e. chunk size is 32B/64B instead of 16B).
But for simplicity we ignore them in this blog.
Now you can kinda see why I stated earlier swizzle doesn’t change the major-ness of the input tile because of this 16B atomicity property.
If the tile in GMEM is K-major (K dimension is the contiguous dimension), the 16B chunk represents 8 K values are contiguous in both GMEM and SMEM after swizzling.
Similarly, if the tile in GMEM is M-major (M dimension is the contiguous dimension), the 16B chunk represents 8 M values are contiguous in both GMEM and SMEM after swizzling.
Swizzle preserves atomicity and it only orders at the 16B chunk granularity.
3.1.3. K-Major Swizzle 64B
Same deal except this time the swizzle atom becomes a 8x64B tile (M=8, K=64B or K=32 assuming bf16 input).
The swizzle 64B atom now contains 32 1x16B chunks or 4 8x16B (required by ldmatrix.m8n8) subtiles (colored in grey, red, purple, and blue).
The chunk order shown on the right makes sure ldmatrix.m8n8 can read each colored 8x16B subtile in 1 cycle without bank conflicts.
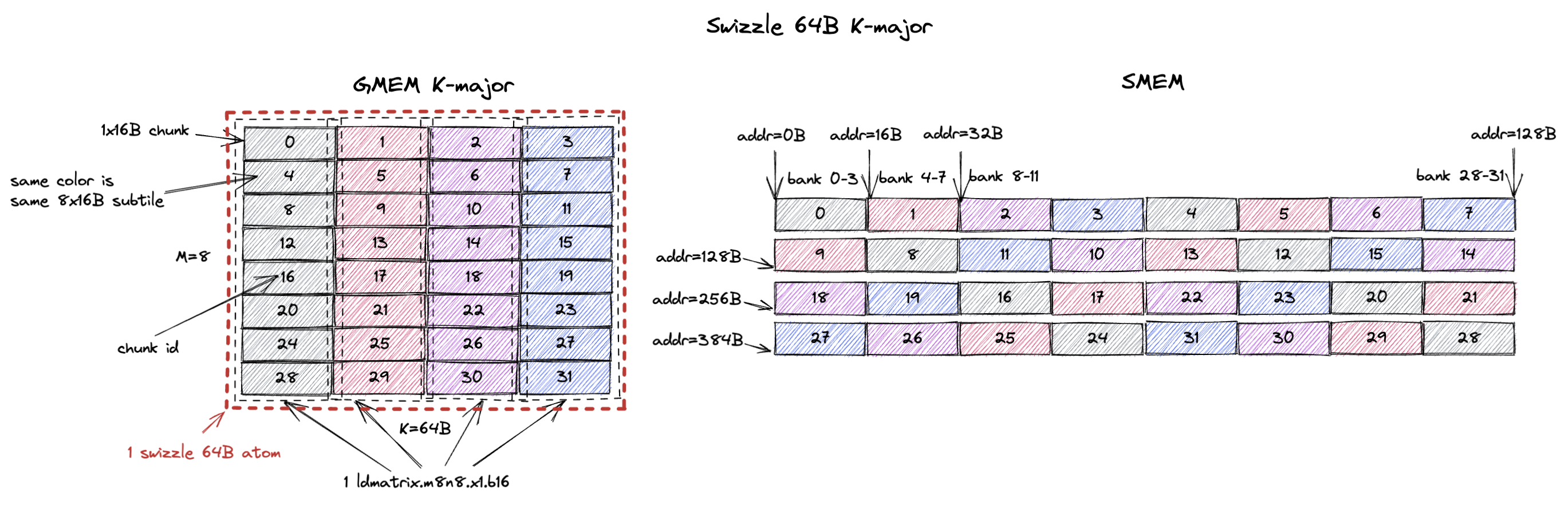
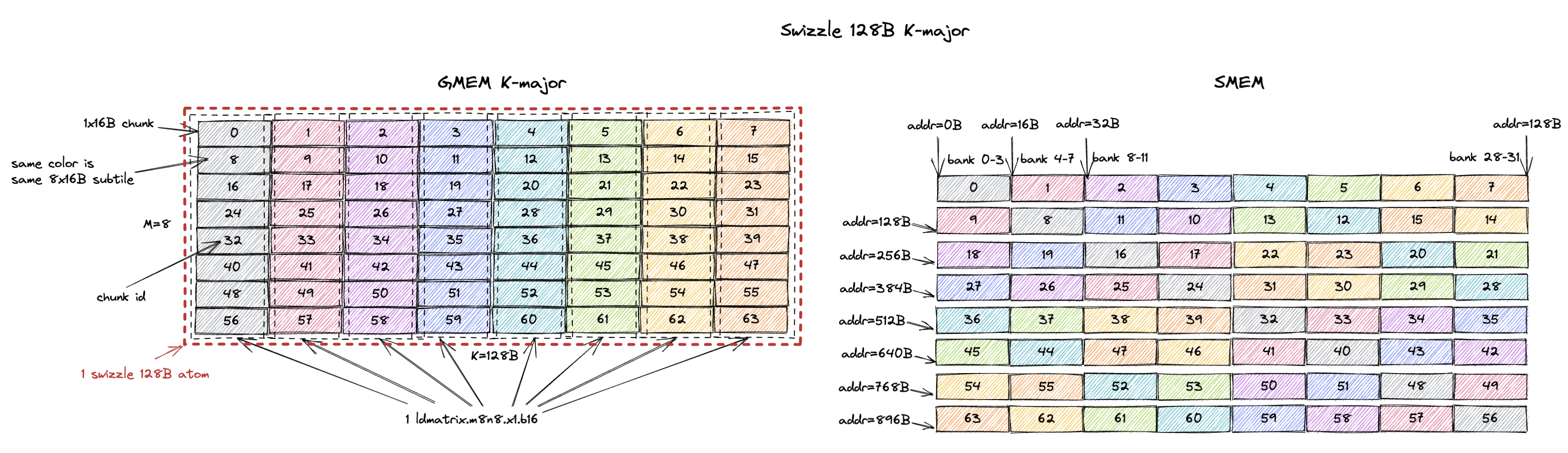
3.1.4. K-Major Swizzle 128B
Swizzle 128B is the most commonly used swizzle layout and we will explain the reason in Sec. 5.
Same deal again, the swizzle atom becomes a 8x128B tile (M=8, K=128B or K=64 assuming bf16 input).
And each 8x16B subtile can be loaded from SMEM in 1 cycle without bank conflicts.
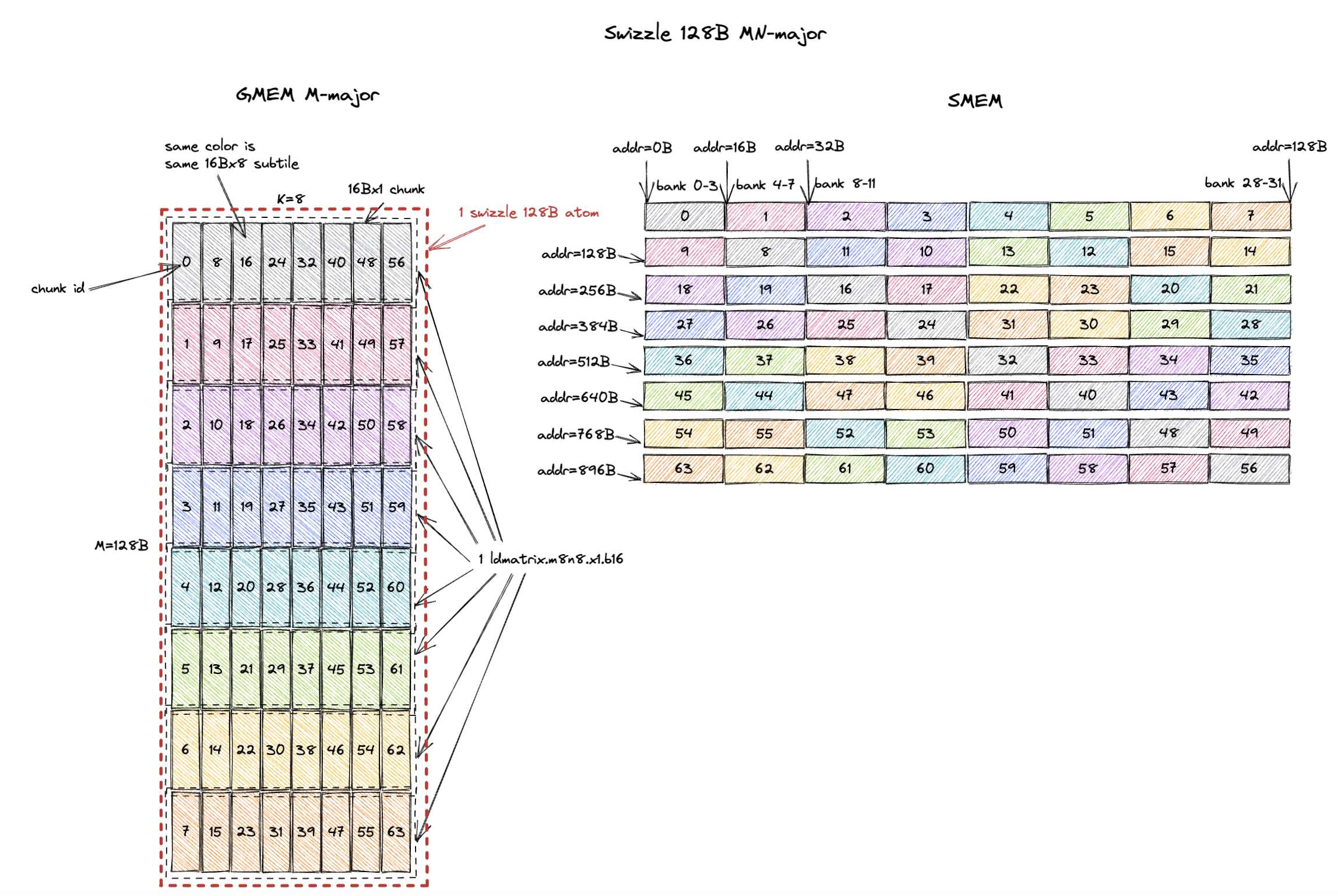
3.2. MN-Major Swizzle Layout
If the GMEM tile is M/N-major, you should choose the MN-major swizzle layout for SMEM.
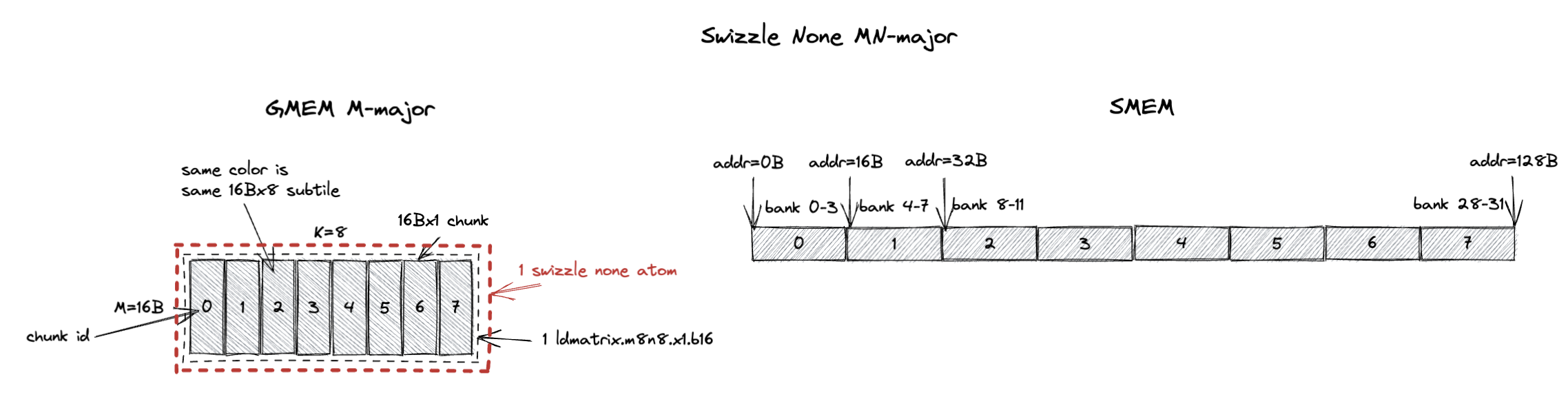
3.2.1. MN-Major Swizzle None
The swizzle atom for MN-major layout is 16Bx8 (M=16B or M=8 assuming bf16 input, K=8).
And each 16Bx1 chunk now contains 8 M values that are contiguous in both GMEM and SMEM after swizzling.
But the 1 cycle/chunk property is not changed.
ldmatrix.m8n8 can still load each 16Bx8 subtile in 1 cycle without bank conflicts, except this time the subtile is MN-major rather than K-major.
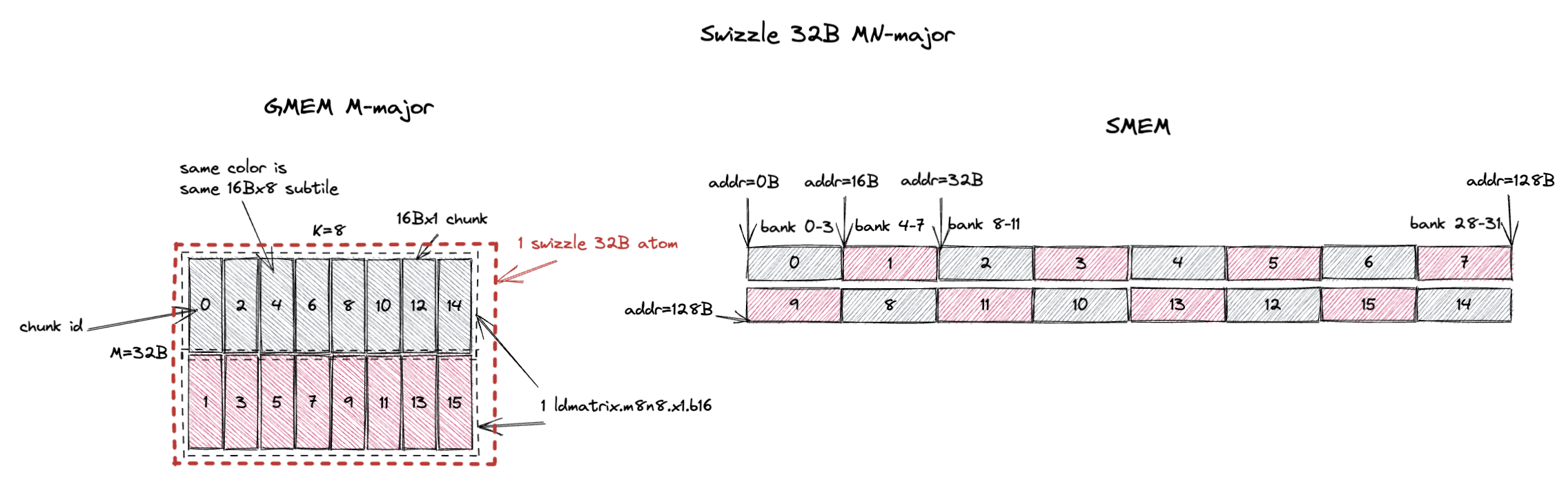
3.2.2. MN-Major Swizzle 32B
Similarly, the swizzle atom becomes 32Bx8 (M=32B or M=16 assuming bf16 input, K=8).
And it contains 16 16Bx1 chunks or 2 16Bx8 subtiles (colored in grey and red).
The swizzle 32B layout ensures that ldmatrix.m8n8 can load each colored 16Bx8 subtile in 1 cycle without bank conflicts.
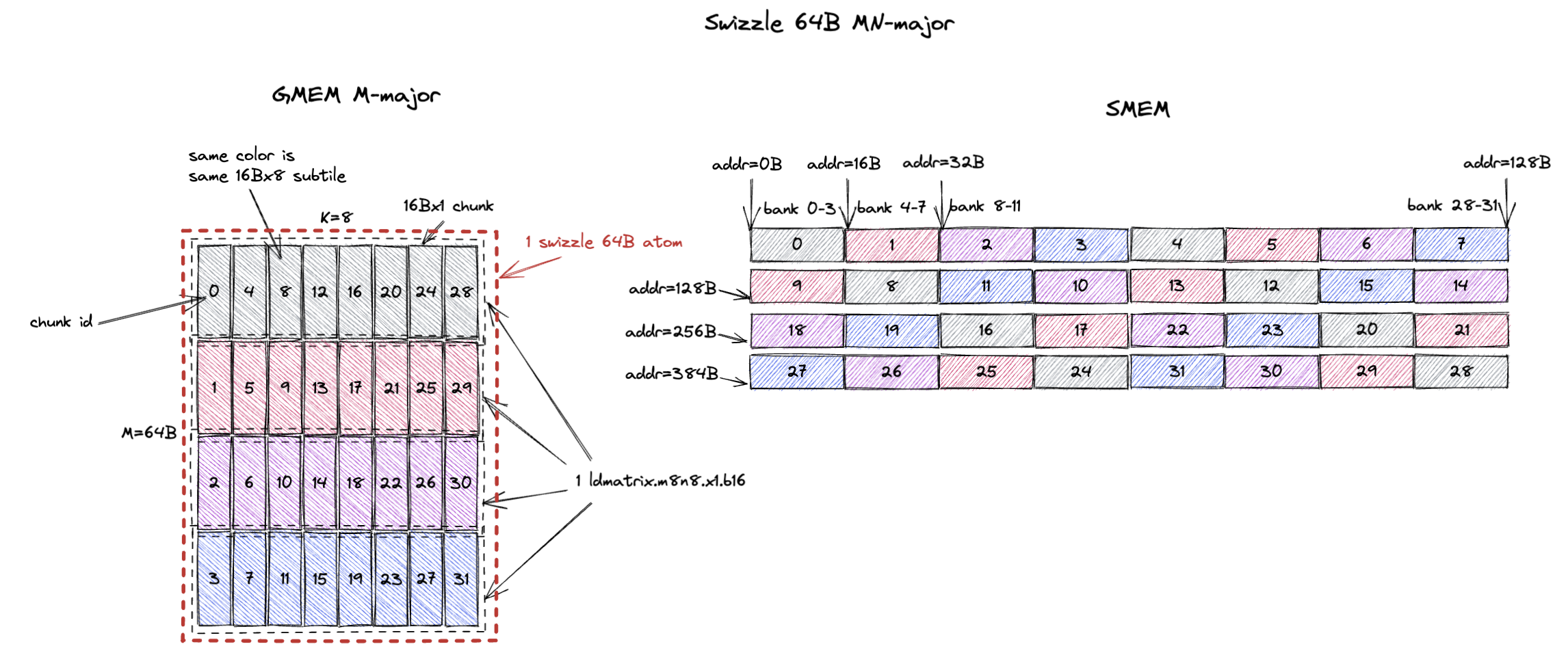
3.2.3. MN-Major Swizzle 64B
For swizzle 64B, the swizzle atom becomes 64Bx8 (M=64B or M=32 assuming bf16 input, K=8).
And it contains 32 16Bx1 chunks or 4 16Bx8 subtiles (colored in grey, red, purple, and blue).
The swizzle 64B layout ensures that ldmatrix.m8n8 can load each colored 16Bx8 subtile in 1 cycle without bank conflicts.
3.2.4. MN-Major Swizzle 128B
Swizzle 128B is the most commonly used swizzle layout and we will explain the reason in Sec. 5.
Same deal again, the swizzle atom becomes a 128Bx8 tile (M=128B or M=64 assuming bf16 input, K=8).
And each 16Bx8 subtile can be loaded from SMEM in 1 cycle without bank conflicts.
4. Why Swizzle?
Now that we know what the swizzle layout is, let’s answer the question why we need to swizzle.
You can already kinda see the reason: it allows the ldmatrix.m8n8 instruction to load a 8x16B/16Bx8 subtile (within a larger tile) in 1 cycle without SMEM bank conflicts.
Below we explain this with a concrete example.
Here I want to stage a M=8, K=32B (or K=16 assuming bf16 input) K-major tile in GMEM to SMEM.
In GMEM, chunk 0, 1 are contiguous and chunk 2, 3 are contiguous, etc.
So a natural SMEM layout is to follow the contiguity of the chunks in GMEM for better copy vectorization.
Each GMEM to SMEM copy consists of 2 chunks (32B) instead of 1 chunk (16B).
We call this the SMEM linear layout.
As shown on the top right of the figure, I just store chunk 0, 1, 2, 3, … contiguously in SMEM.
But you can immediately see the problem of this layout: the ldmatrix.m8n8 instruction cannot load a 8x16B subtile in 1 cycle without SMEM bank conflicts.
If I load the grey subtile, it will load chunk 0, 2, 4, 6, 8, 10, 12, 14, they are all stored in half of the SMEM banks.
This will cause 2-way bank conflicts.
Now let’s see what will happen if we use the swizzle 32B layout.
The M=8, K=32B is exactly the size of 1 swizzle 32B atom.
And when we access the grey subtile, it will load chunk 0, 2, 4, 6, 8, 10, 12, 14, they are all stored in different SMEM banks.
The same is true for the red subtile.
So the ldmatrix.m8n8 instruction can load both the grey and red subtiles in 1 cycle without bank conflicts.
Swizzling avoids bank conflicts when ldmatrix.m8n8 loads a 8x16B subtile.
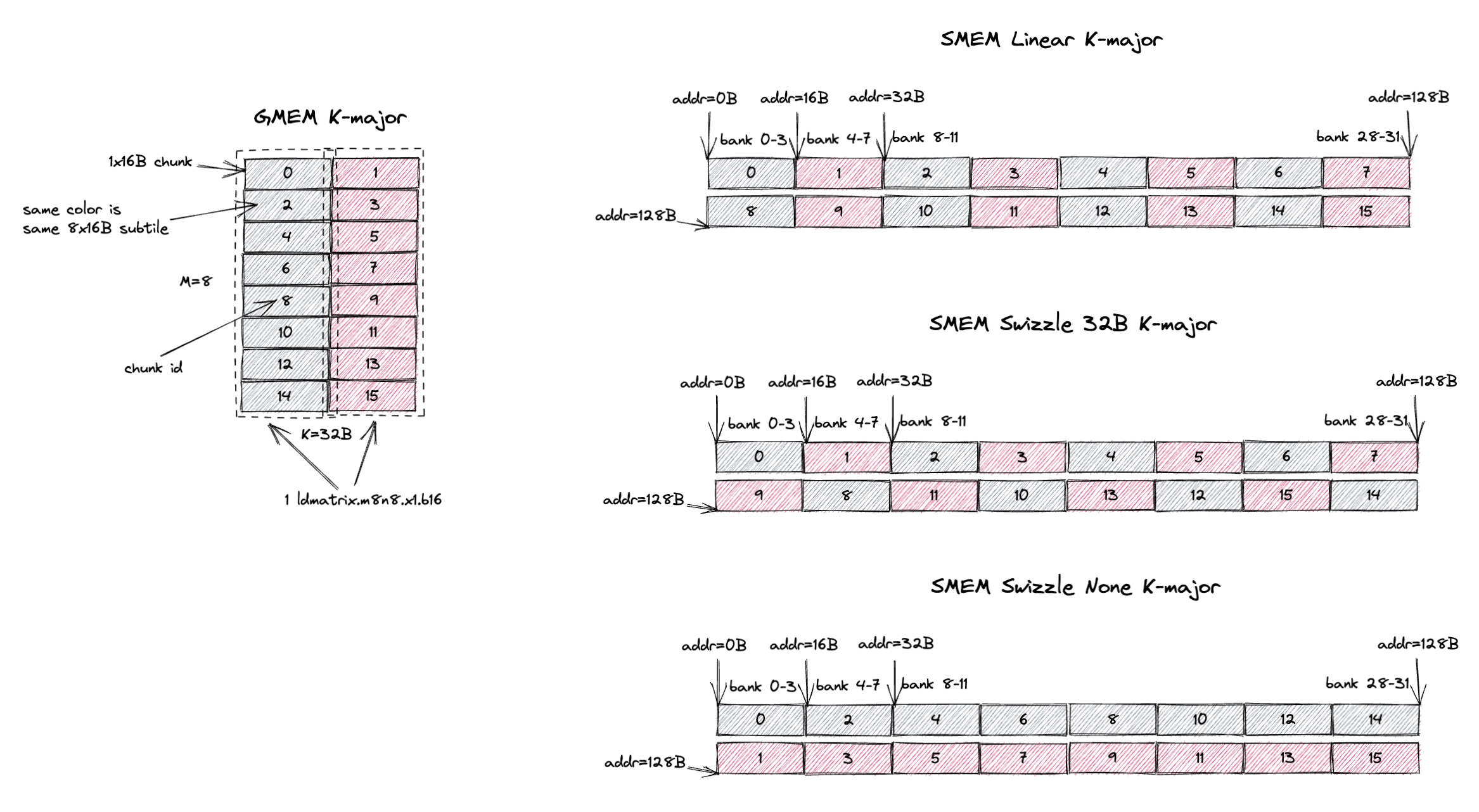
The swizzle none layout can also avoid bank conflicts when ldmatrix.m8n8 loads a 8x16B subtile.
But it requires the M=8, K=8 K major subtile to be stored contiguously in SMEM.
Confusingly, this is different from the SMEM linear layout we mentioned above.
Even though it’s called swizzle none, it’s not the intuitive linear SMEM layout you would expect.
5. Which Swizzle Atom to Choose?
From the example of Sec. 4, we can see that both swizzle none and swizzle 32B layouts can avoid bank conflicts when ldmatrix.m8n8 loads a 8x16B subtile.
But why would I choose one over the other?
It’s because there will have different GMEM access efficiency.
Below we give an example to show the performance difference between different swizzle layouts.
The tile we are trying to load into SMEM is M=8, K=64B (or K=32 assuming bf16 input) K-major tile.
We compare 3 swizzle layouts: K-major swizzle none, K-major swizzle 32B, and K-major swizzle 64B shown on the right.
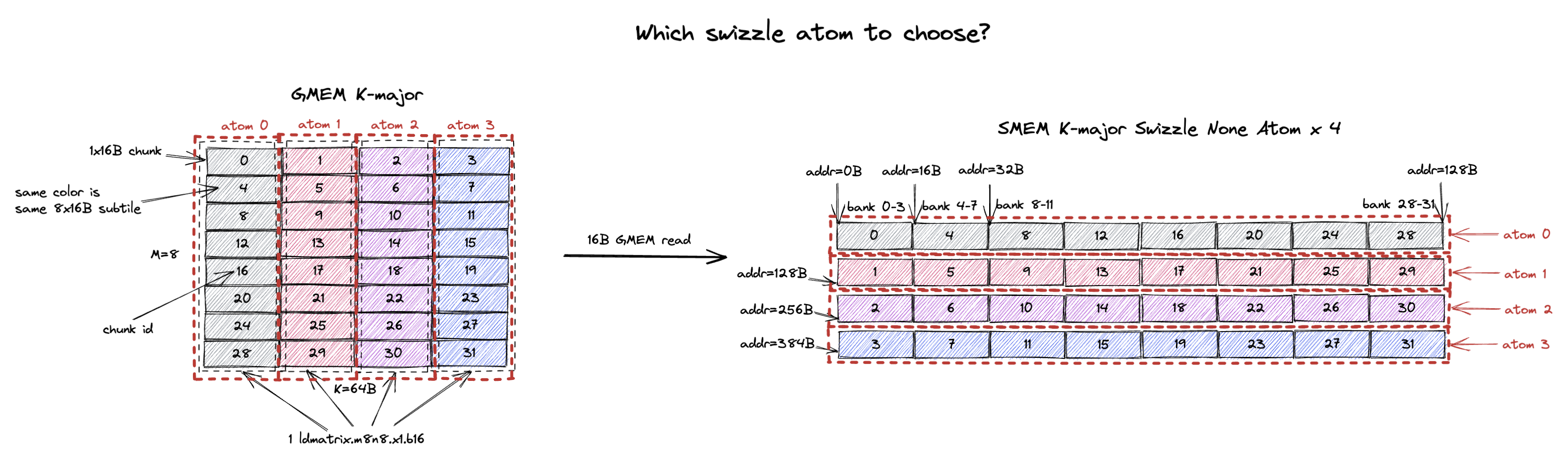
The 8x64B tile contains 32 1x16B chunks or 4 8x16B subtiles (colored in grey, red, purple, and blue).
It will also be constructed from 4 swizzle none atoms, 2 swizzle 32B atoms, or 1 swizzle 64B atom.
The GMEM to SMEM copy can be done in many ways:
ld.global: GMEM->RF,st.shared: RF->SMEM- TMA load: GMEM->SMEM
We focus on the ld.global + st.shared path since TMA really just hardens that flow in hardware.
When using swizzle none layout, we want st.shared to not have any bank conflicts to maximize the SMEM write bandwidth.
So each thread will store 4B to different banks in SMEM and all 32 threads will work on 128B contiguous data in SMEM, i.e. chunk 0, 4, 8, …, 28.
Then these 32 threads needs to load chunk 0, 4, 8, …, 28 from GMEM to RF.
But because the GMEM tile is K-major, only a single 16B chunk is contiguous in GMEM.
When reading chunk 0, 4, 8, …, 28 out, we will have 16B GMEM read requests.
The same is true for other 128B rows of the SMEM, the GMEM read granularity will be 16B.
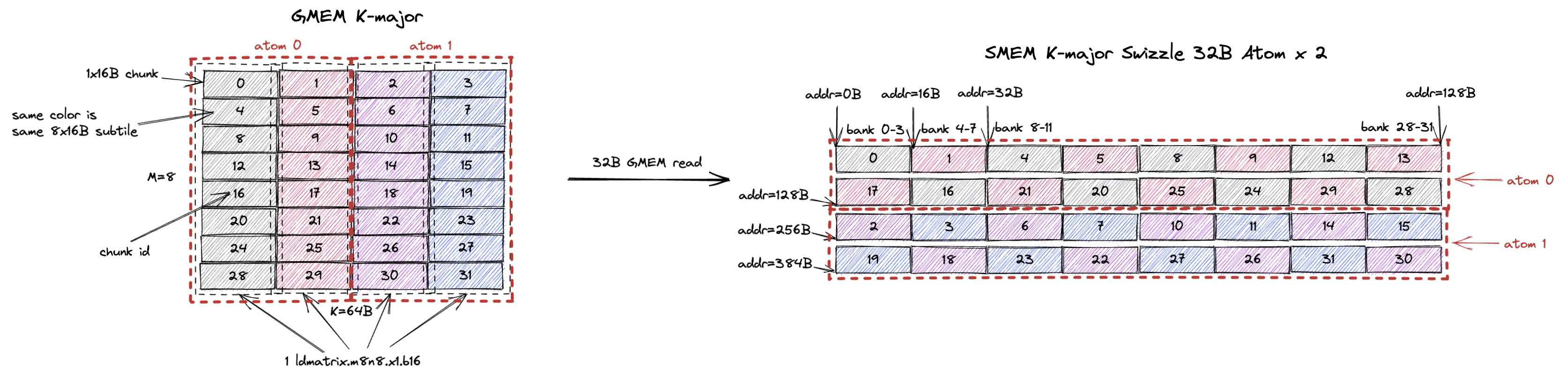
When using swizzle 32B layout, similarly we want to avoid bank conflicts in st.shared.
So all 32 threads will work on chunk 0, 1, 4, 5, 8, 9, 12, 13.
The GMEM load can now happen 2 chunk at a time, i.e. 32B GMEM read requests.
For the other 128B rows of the SMEM, the GMEM read granularity will be 32B.
You can already see the trend, when using swizzle 64B layout, the 32 threads will read chunk 0, 1, 2, 3, 4, 5, 6, 7 from GMEM.
The GMEM load granularity is 64B.
Similarly, for row 2, chunk 9, 8, 11, 10, 13, 12, 15, 14 will be read from GMEM with the same 64B request granularity.
GPU has 128B cacheline size, so reading contiguous 128B of data best utilize the GMEM bandwidth. As we can see from the above example:
swizzle nonelayout generates 16B GMEM read requestsswizzle 32Blayout generates 32B GMEM read requestsswizzle 64Blayout generates 64B GMEM read requests
So in this example, K-major swizzle 64B layout can achieve the best GMEM access efficiency.
And obviously swizzle 128B generates 128B GMEM read requests.
But we can’t use it because the tile size we want is only 64B on the K dimension.
If we want a 8x128B tile, swizzle 128B is the best choice.
So you should always try to use swizzle 128B layout if possible.
The goal of choosing the swizzle layout is to maximize the GMEM read efficiency. That is, given a tile size, one should use the largest possible swizzle atom that can fit the tile:
- If the tile size is
K=16BK-major,K-major swizzle noneis the best choice. And will generate 16B GMEM read requests. - If the tile size is
K=32BK-major,K-major swizzle 32Bis the best choice. And will generate 32B GMEM read requests. - If the tile size is
K=64BK-major,K-major swizzle 64Bis the best choice. And will generate 64B GMEM read requests. - If the tile size is
K>=128BK-major,K-major swizzle 128Bis the best choice. And will generate 128B GMEM read requests. - If the tile size is
M/N=16BMN-major,MN-major swizzle noneis the best choice. And will generate 16B GMEM read requests. - If the tile size is
M/N=32BMN-major,MN-major swizzle 32Bis the best choice. And will generate 32B GMEM read requests. - If the tile size is
M/N=64BMN-major,MN-major swizzle 64Bis the best choice. And will generate 64B GMEM read requests. - If the tile size is
M/N>=128BMN-major,MN-major swizzle 128Bis the best choice. And will generate 128B GMEM read requests.
The above rule is exactly what’s implemented in Cutlass sm100_smem_selector to select the best SMEM swizzle layout.
6. How Transposed Input is Handled?
According to the ptx specification of mma.sync.aligned.m16n8k8.row.col.f32.bf16.bf16.f32 instruction, the A matrix ([M, K]) is row major (K-major) and the B matrix ([K, N]) is column major (K-major).
What will happen if my A matrix is M-major in GMEM?
Where does the transpose of A happen before being fed into the tensor core?
The answer is that ldmatrix will do the optional transpose (i.e. the trans suffix) of A before feeding it into the tensor core, the swizzling layout is irrelevant here.
Let’s first understand how non-transposed (K-major) A matrix is handled.
The input tile size for the bf16 mma.m16n8k8 is M=16, K=8 or K=16B as shown on the left.
Because tile K is only 16B, we use K-major swizzle none layout for SMEM and this tile contains 2 swizzle none atoms.
Each ldmatrix.m8n8 instruction will load a 8x16B subtile from SMEM into RF.
The first load is to the grey chunks 0, 1, 2, 3, 4, 5, 6, 7 and the register fragment value is shown at the bottom right.
For example, thread 0 (T0) will hold M0K0, M0K1, M0K2, M0K3.
T22 will hold M5K4, M5K5, M5K6, M5K7.
This is exactly what the mma instruction expects the input fragment layout to be (as draw in Sec. 2.1).
Now let’s see how M-major A matrix is handled.
The input tile size for the bf16 mma.m16n8k8 is still M=32B or M=16, K=8 as shown on the left.
Because tile M is 32B, we use M-major swizzle 32B layout for SMEM and this tile contains 1 swizzle 32B atoms.
If we do nothing, each ldmatrix.m8n8 instruction will load a 16Bx8 subtile from SMEM into RF.
The first load is to the grey chunks 0, 2, 4, 6, 8, 10, 12, 14 and the register fragment value is shown at the bottom left.
Then T0 holds M0K0, M1K0, M2K0, M3K0.
T22 holds M4K5, M5K5, M6K5, M7K5.
This is not what the mma instruction expects the input fragment layout to be, it’s the transpose of the required layout.
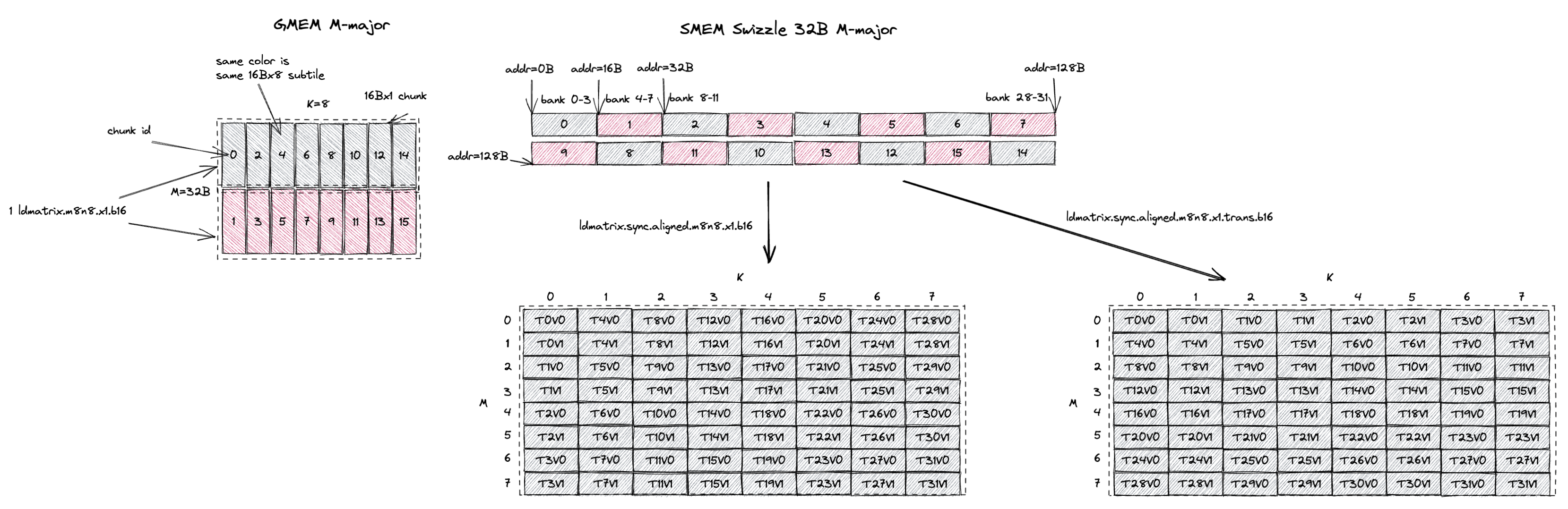
So here comes ldmatrix.m8n8.trans that transposes the 16Bx8 tile during SMEM->RF copy.
If we use the transpose version of ldmatrix, the first load is still going to be the grey chunks 0, 2, 4, 6, 8, 10, 12, 14 and the register fragment value is shown at the bottom right.
Now T0 holds M0K0, M1K0, M2K0, M3K0.
T22 holds M4K5, M5K5, M6K5, M7K5.
This is exactly what the mma instruction expects the input fragment layout to be.
To summarize, if the input is MN-major in SMEM/GMEM, ldmatrix will do the optional transpose (i.e. the trans suffix) of input such that the input values in RF are in the required K-major layout.
6.1. Difference with Bank Conflict Free Matrix Transpose
Again very confusingly, you may hear before one can use swizzling to do bank conflict free matrix transpose.
But here I tell you the transpose happens during the SMEM->RF copy of ldmatrix and has nothing to do with SMEM swizzle layout.
Unfortunately both statements are true (that’s why it’s so confusing!).
The mma swizzle layout has 16B atomicity (32B/64B atomicity in corner cases we won’t cover). The swizzle layout required to do bank conflict free matrix transpose is normally 4B atomicity (assuming fp32 input). So they are both swizzle layout but with different atomicity/configuration.
But the spirit is the same, take K-major swizzle 64B as an example, it allows bank conflict free access to both 2x64B (needed for st.shared during GMEM->SMEM copy) and 8x16B (needed for ldmatrix.m8n8 during SMEM->RF copy) subtiles of a larger 8x64B tile/atom.
For matrix transpose, the swizzle layout allows bank conflict free access to a row (1x128B) or a column (32x4B) of the input matrix tile.
Swizzle layout allows bank conflict free access to subtiles of two different shapes.
You can read more about bank conflict free matrix transpose in Lei Mao’s blog or Colfax research’s blog.
7. Swizzle Atom Layout
So far we’ve mostly looked at small tile sizes that contains only 1 or a few swizzle atoms.
The natural next question is what’s the layout of the swizzle atom when the tile size is larger than the swizzle atom size?
Below we show an example of a M=16, K=64B (or K=32 assuming bf16 input) K-major tile and how different swizzle atoms can be laid out to form the tile.
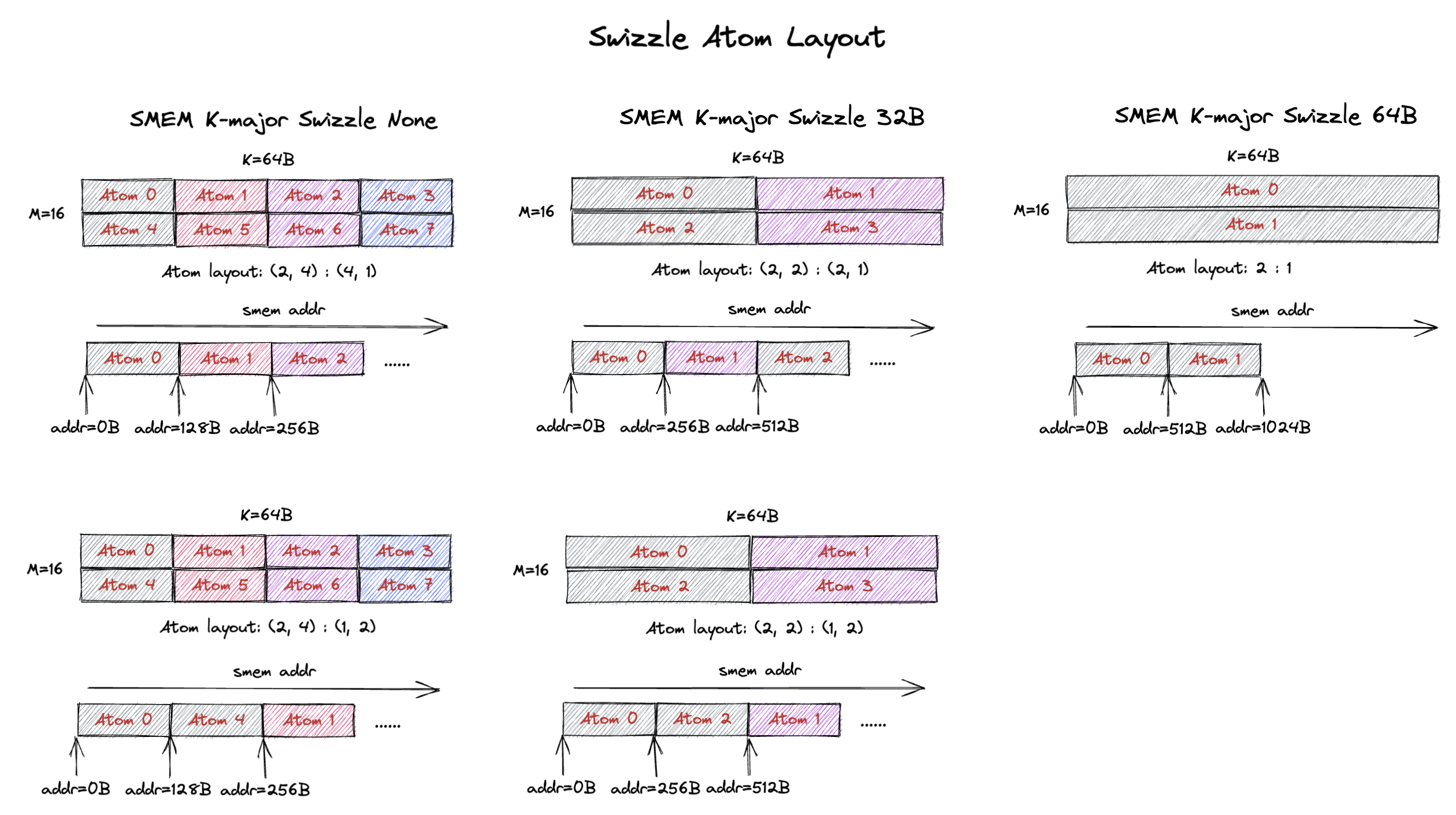
The 16x64B tile contains 8 swizzle none atoms.
These atoms are laid out in a 2x4 grid as shown on the left.
But the atom layout can be row-major (top) or column-major (bottom).
For row-major atom layout, the atoms in the same row are contiguous in SMEM (e.g. atom 0, 1, 2, 3).
For the column-major atom layout, the atoms in the same column are contiguous in SMEM (e.g. atom 0, 4).
Similarly, the 16x64B tile contains 4 swizzle 32B atoms.
You can also lay out the atoms in a 2x2 grid in both row-major and column-major layout (middle of the figure).
That renders different atom contiguity patterns in SMEM.
As a kernel author, you should be able to use any of the swizzle atom layout and get the correct result. CuTe should abstract away the different address calculation for different swizzle atom layouts.
8. What about Hopper and Blackwell?
So far we’ve only talked about Ampere mma and hopefully I convinced you the combination of swizzle layout and ldmatrix feeds the correct data to the Ampere tensor core.
Hopper and Blackwell mma can source input directly from SMEM with no ldmatrix involved.
How do they understand the different swizzle atom and swizzle atom layouts?
These information is encoded in the SMEM matrix descriptor (that CuTe can build for you automatically too).
You can refer to Hopper mma matrix descriptor and Blackwell mma matrix descriptor for more details.
Soon I’ll cover the blackwell part in more details in a separate blog using a low-latency optimized blackwell GEMM kernel I wrote and open sourced in FlashInfer.
Stay tuned :)
9. Compatibility with TMA
Hopper introduces Tensor Memory Accelerator (TMA) to facilitate tensor data movement between GMEM and SMEM. TMA supports loading the tile to SMEM with the swizzling the subsequent MMA expects. So in this section, we will explain how to use TMA to load the sizzled layout that can be directly consumed by the Tensor Core.
Nominally, CuTe handles all these for you correctly and magically. But it’s good to understand what happens under the hood in case you have some custom cases where you want to bypass CuTe.
If you want to inspect what’s the TMA box size that CuTe will create for you given a tile size and swizzle layout, you can use the test_tma program and add some code to print out the created TMA descriptor here.
9.1. TMA Swizzle None
The swizzled layout supported by TMA is mostly compatible with the mma swizzle layout we’ve described above.
But there are minor nuances.
And the most important difference is Swizzle None layout means slightly different things for TMA and MMA.
The figure below explains the difference as well as how to use Swizzle None mode in TMA to correctly feed the data to the Tensor Core.
We start with an example tile of K-major 8x64B tile in GMEM and it will be the A operand of the mma.sync.aligned.m16n8k8.row.col.f32.bf16.bf16.f32 instruction.
Here we explicitly want to use K-major Swizzle None SMEM layout for the MMA.
The first row of the figure describes the actual SMEM layout.
The 8x64B tile is broken down into 4 8x16B Swizzle None atoms.
And each atom (128B) is stored contiguously in SMEM.
We can just use a simple ld.global to do 16B GMEM read requests to load the entire tile into SMEM.
And the subsequent MMA will correctly consume the tile in SMEM using the ldmatrix.m8n8 instruction.
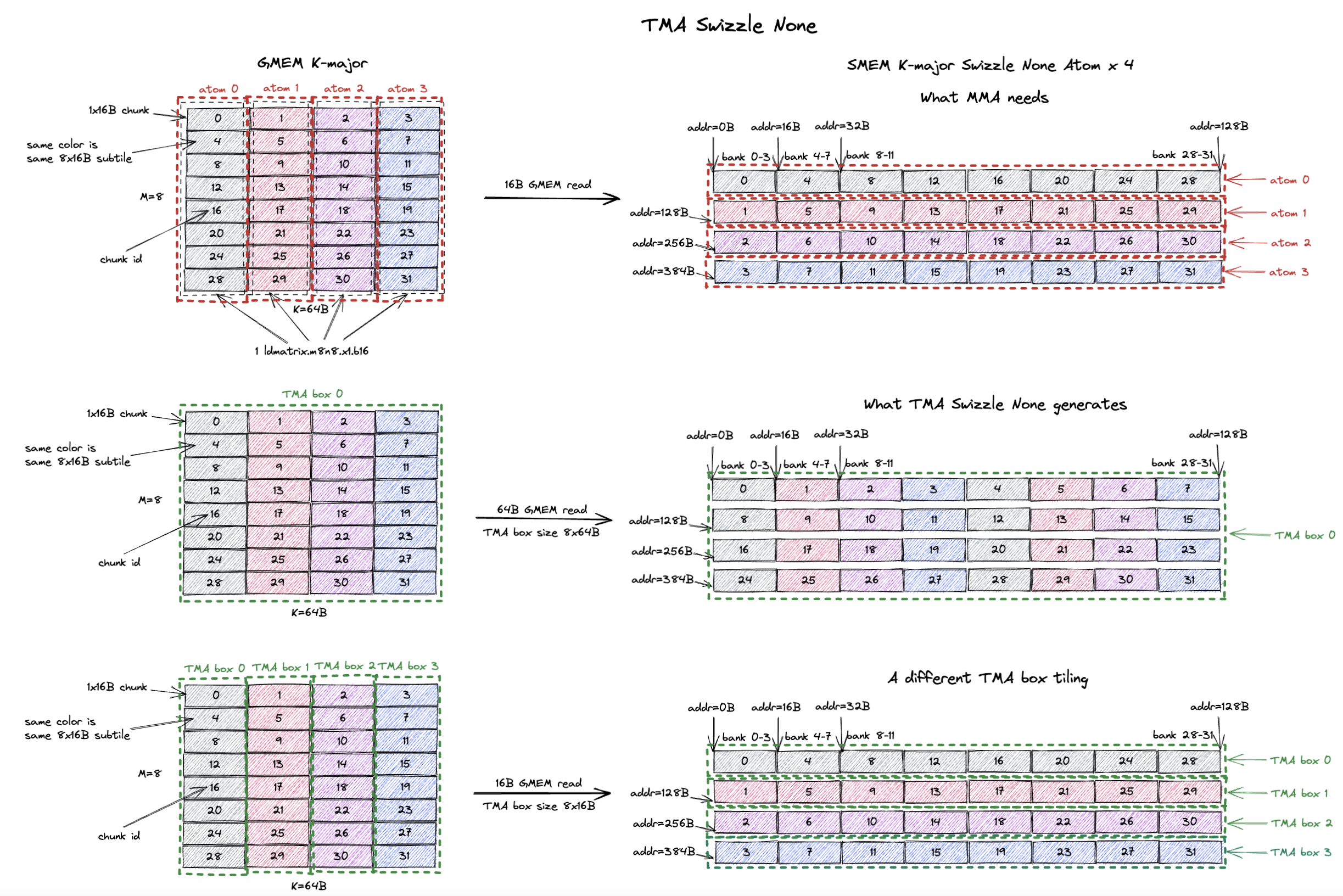
Now let’s say I want to use TMA instead of ld.global to load the tile into SMEM.
And we can leverage the TMA Swizzle None mode.
This is what the second row of the figure shows.
We declare a TMA box of size 8x64B (i.e. the entire tile) and set the Swizzle None mode.
What TMA would do is it would:
- load the first row (64B) of the box from GMEM (i.e. chunk 0, 1, 2, 3) and store them contiguously in SMEM.
- load the second row (64B) of the box from GMEM (i.e. chunk 4, 5, 6, 7) and store them contiguously in SMEM.
- load the third row (64B) of the box from GMEM (i.e. chunk 8, 9, 10, 11) and store them contiguously in SMEM.
- …until the last row (64B) of the box is loaded.
This creates nice 64B GMEM read requests which is nice.
However, as we can see on the right, this SMEM layout is not what ldmatrix.m8n8 expects!
The tensor core expects the SMEM layout to be chunk 0, 4, 8, 12, 16, 20, 24, 28…, but with TMA box size of 8x64B, we get chunk 0, 1, 2, 3, 4, 5, 6, 7… as the SMEM layout.
The Swizzle None SMEM layout TMA produces is incompatible with the Swizzle None SMEM layout the tensor core expects.
There are ways to fix this, i.e. we can create a specific TMA box size such that the Swizzle None mode of TMA and MMA are compatible.
The key is the width of the TMA box (the dimension where you have the swizzling, i.e. the major/contiguous dimension) should be exactly the same as 1 swizzle atom width. You can extend the TMA box height however you want (multiple of 8).
Another way to put this is you can stack many swizzle atoms on top of each other vertically (for K major layout) to form the TMA box.
But you can’t stack more than 1 swizzle atom horizontally (for K major layout) to form the TMA box.
The last row of the figure shows the correct TMA box size that makes the Swizzle None mode of TMA and MMA compatible.
Basically we create a TMA box of size 8x16B (exactly 1 Swizzle None atom).
If the tile is taller (e.g. 16x64B), we can stack 2 Swizzle None atoms vertically to form the 16x16B TMA box.
But again you can’t form a 8x32B TMA box because the box width is larger than 1 Swizzle None atom width (16B) and will create incompatible SMEM layout.
As you can see in the figure, TMA copies the data in the box row by row, and put each box row contiguously in SMEM.
So TMA box 0 will copy chunk 0, 4, 8, 12… to SMEM contiguously.
The whole 8x64B tile will be broken down into 4 8x16B TMA boxes and we copy it box by box to SMEM.
The final SMEM layout is exactly the same as the Swizzle None SMEM layout the tensor core expects and equivalent to the ld.global case.
But you can see the inefficiency here, each TMA transfer will do 16B GMEM read requests.
9.2. TMA Swizzle
We use the same example of 8x64B tile but this time we want to use K-major Swizzle 32B layout for the MMA because we want to improve the GMEM access efficiency.
Swizzle None case we only generate 16B GMEM read requests.
The first row of the figure below shows the baseline ld.global implementation.
The tile is broken down into 2 8x32B Swizzle 32B atoms and we copy it atom by atom to SMEM.
The GMEM read efficiency improves to 32B GMEM read requests.
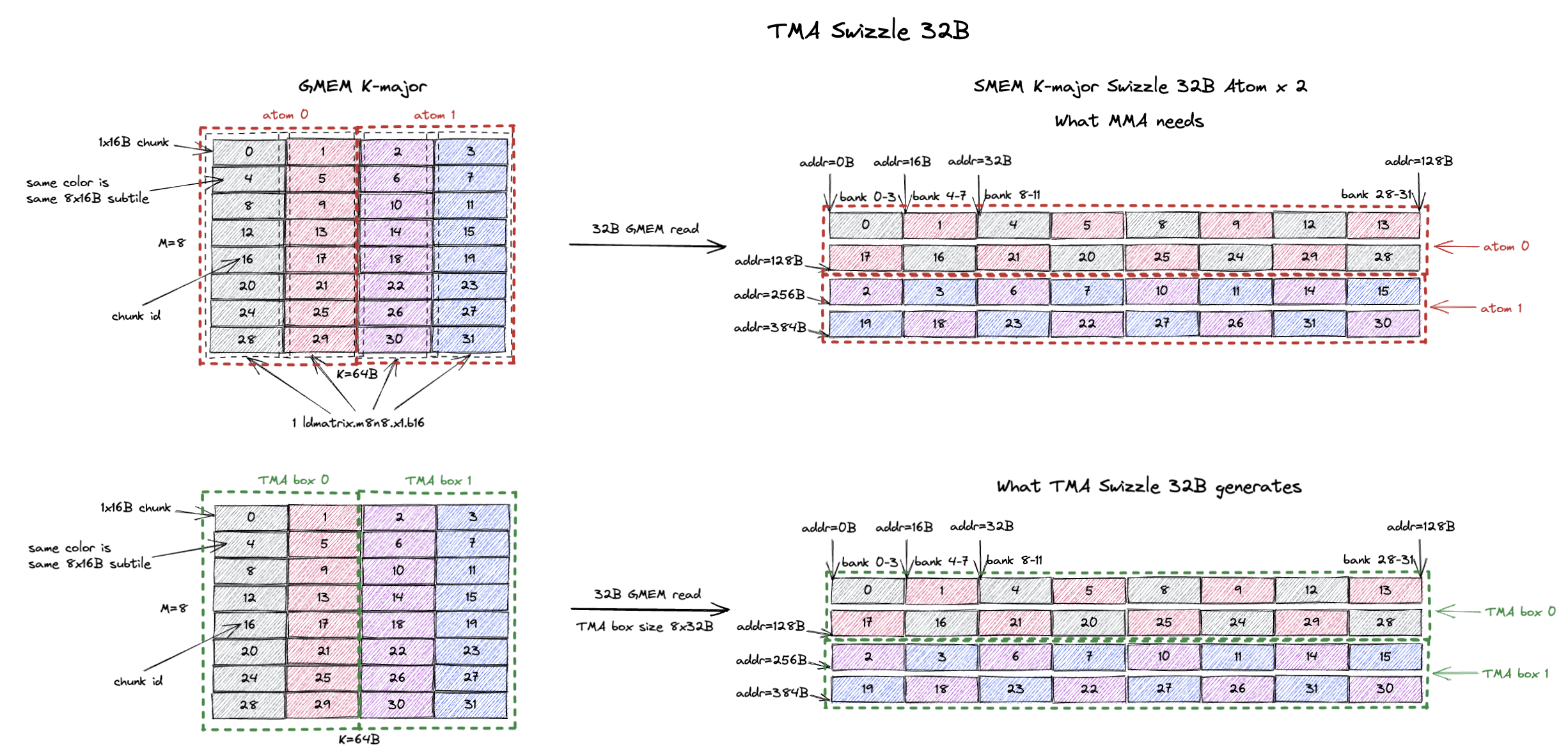
Similarly, we can use TMA to achieve this as long as the TMA box width is exactly the same as 1 Swizzle 32B atom width (32B).
The second row of the figure shows exactly that.
We have a TMA box of size 8x32B (exactly 1 Swizzle 32B atom) and the tile consists of 2 8x32B TMA boxes.
TMA will read box 0 from GMEM and put rows of box 0 contiguously in SMEM (i.e. chunk 0, 1, 4, 5, 8, 9…).
Setting TMA swizzle mode to Swizzle 32B, it will also apply the appropriate swizzling to the 16B data chunks.
The end result SMEM layout on the right is exactly the same as the ld.global case.
So we have correct swizzled layout for the MMA and now the GMEM access efficiency is improved to 32B GMEM read requests.
Reinforcing the idea again, the TMA box can be arbitrarily high (e.g. 16x32B or 32x32B), but the width of the TMA box should be exactly the same as 1 swizzle atom width.
Other swizzle layouts (64B and 128B) follow the exact same usage pattern.
This is exactly why if you have a 64x256B tile, and you use Swizzle 128B layout, inspecting the ptx/SASS instruction you will see 2 TMA load instructions rather than 1.
Because CuTe will create the maximum TMA box size of 64x128B and break the tile into 2 TMA boxes.
Then we issue 2 TMA load instructions to load the tile into SMEM with MMA compatible swizzled layout.
9.3. Putting it all together
Now that we’ve understand how to create a MMA compatible TMA box, let’s apply it to a real problem size on Blackwell.
The Blackwell Tensor Core (tcgen05.mma) requires M=64 or M=128 and each instruction process K=32B.
Given a K-major 64x64B tile, we want to load it to SMEM to feed the Tensor Core using TMA.
The figure below shows the use case.
This 64x64B tile is going to be processed by 2 tcgen05.mma instructions (grey and pink subtiles in the figure).
As an example, we want to use K-major Swizzle 32B layout for the SMEM (obviously we can use other swizzle layouts too).
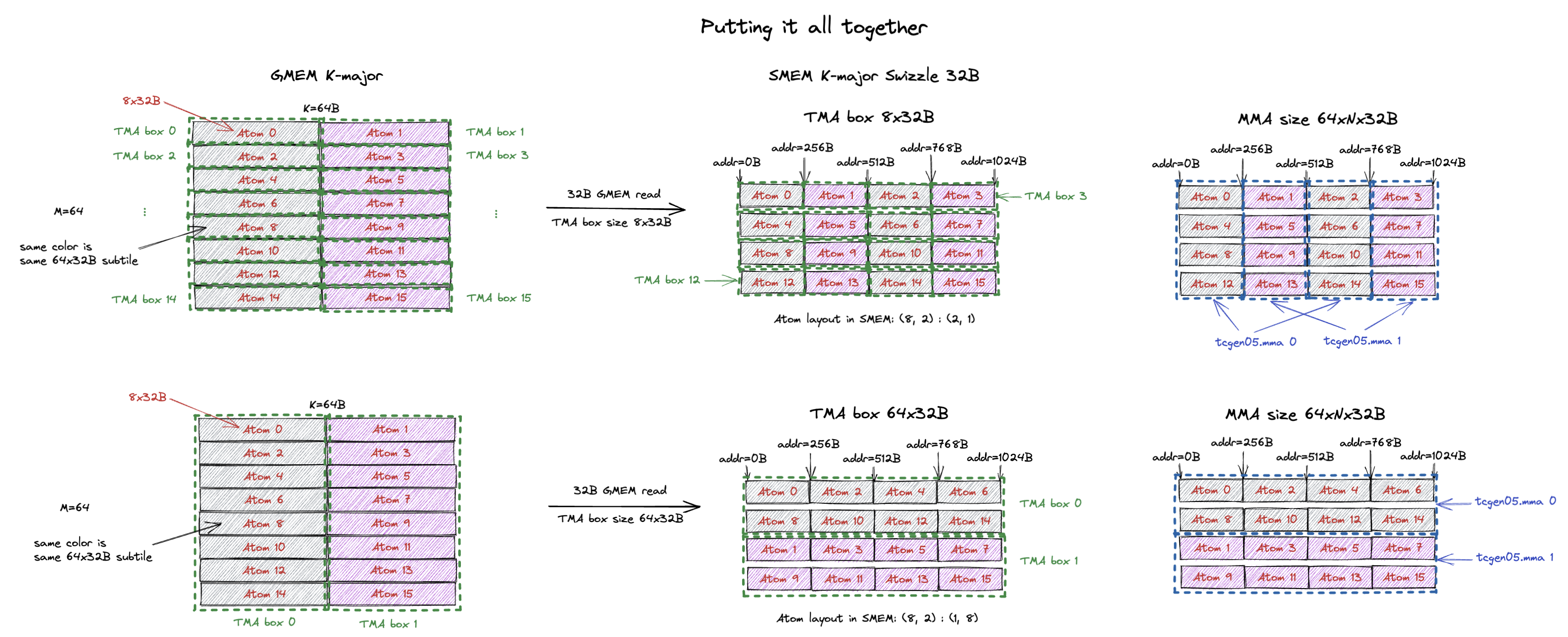
As we have explained in Sec. 7, we can stack the Swizzle 32B atoms in row-major or column-major layout to form the final SMEM layout for the tile.
The first example shows the row-major stacking, i.e. atom 0, 1, 2, 3 are contiguous in SMEM.
We want to use TMA to fill the SMEM.
Notice that the max TMA box we can use is just 8x32B (a single Swizzle 32B atom).
Because TMA puts atoms in the same TMA box contiguously in SMEM.
Given the end SMEM layout we want, we can’t have a taller TMA box (e.g. 16x32B because atom 0 and 2 would be in the same TMA box and thus contiguous in SMEM.).
We also can’t have a wider TMA box because the layout would be incompatible with what the tensor core expects.
Hence we have 16 TMA boxes for the 64x64B tile and generates 32B GMEM read requests.
The blue box on the top right corner shows the swizzle atom needed by a single tcgen05.mma instruction.
MMA 0 needs atom 0, 2, 4, 6… and MMA 1 needs atom 1, 3, 5, 7…
The layout of MMA 0’s input operand (atom 0, 2, 4, 6… (64x32B subtile)) can be described as a Blackwell mma matrix descriptor and CuTe can build it for you automatically.
If we stack the swizzle atoms in column-major layout (i.e. atom 0, 2, 4, 6… are contiguous in SMEM), we can have a much larger TMA box.
The bottom of the figure illustrates the column-major stacking.
We can have a TMA box size of 64x32B (which includes atom 0, 2, 4, 6, 8, 10, 12, 14).
After the TMA transfer, atom 0, 2, 4, 6, 8, 10, 12, 14 will be contiguously in SMEM, exactly what we specified!
Now the 64x64B tile simply contains 2 64x32B TMA boxes and we issue only 2 (instead of 16 in the row-major case) TMA load instructions to load the tile into SMEM with 32B GMEM read requests.
The blue box on the bottom right corner shows the swizzle atom needed by a single tcgen05.mma instruction.
MMA 0 needs atom 0, 2, 4, 6… and MMA 1 needs atom 1, 3, 5, 7…
The layout of MMA 0’s input operand (atom 0, 2, 4, 6… (64x32B subtile)) can also be described as a Blackwell mma matrix descriptor.
Note that the only layout difference of these two subtiles is the stride between two swizzle atoms, and this is exactly what Stride Dimension Byte Offset specifies.
In summary, different swizzle atom layouts can issue different number of TMA instructions to load the tile into SMEM. But both layouts will yield the correct result.
10. Summary
In this blog I covered mostly what you need to know about mma swizzle layout:
- The 8 legal mma swizzle layouts and their specifications.
- Swizzle layout makes sure when the tile is copied from GMEM to SMEM and read out from SMEM (
8x16Bor16x8B), there is no SMEM bank conflicts. - Swizzling doesn’t change the major-ness of the input tile when loading from GMEM to SMEM, it only changes how the 16B chunk are laid out in SMEM.
- Maximizing swizzle atom size improves GMEM access efficiency (longer contiguous loads).
- Transpose happens during SMEM->RF copy of
ldmatrixand is not handled by swizzle layout. - Swizzle atom layout in SMEM can be arbitrary and should always yield the correct result, but some layouts are more efficient than others.
- TMA supports loading the swizzled layout that can be directly consumed by the Tensor Core, with the caveat that the width of the TMA box should be exactly the same as 1 swizzle atom width.